日本の数学【和算】
　江戸時代に日本独自の数学が発達し、「和算」とよばれています。
　中国からそろばんが入ってきて、そろばんを使ったわり算のしかたの本が出版されたり、生活の中での問題が作られたり、いろいろな長さや面積を求める問題が作られたりしました。
　そして、人々がくふうをこらした問題を作り、「算額（さんがく）」として神社にかかげることも行われました。
　円周率を12けたまで求めた関孝和（せきたかかず）も、和算の発達に力をつくした人です。また、吉田光由（よしだみつよし）という人が書いた「塵劫記（じんこうき）」という和算の本は、多くの人に読まれました。
　和算のススメ！（和算とは、和算の教科書、算額というもの、世界的な大数学者　関孝和、和算の衰退、再び光が、子どもたちに和算を教える意義：和田陽子）

塵劫記問題1：４人が6里の道を行くのに、馬が3頭いる。同じ道のりずつ乗るには、どのように乗ればよいか。（1里は今の約4km）　また、次のような問題の出ている本もあります。単位は、現在使われているものに直してあります。

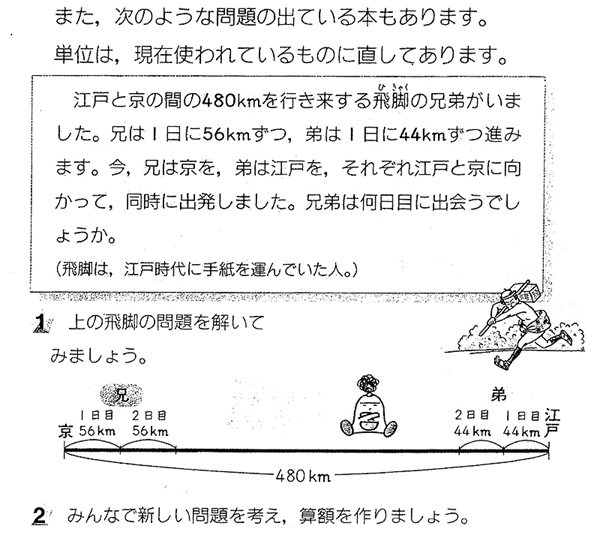
塵劫記問題2：江戸と京の間の480kmを行き来する飛脚（ひきゃく）の兄弟がいました。兄は1日に56kmずつ、弟は1日に44kmずつ進みます。今、兄は京を、弟は江戸を、それぞれ江戸と京に向かって、同時に出発しました。兄弟は何日目に出会うでしょうか。（飛脚は、江戸時代に手紙を運んでいた人。）

和算にチャレンジ！
問題1　鶴亀算
つるとかめ合わせて、頭が13で、足の数が42本、つる、かめはそれぞれ何びき(羽)いるか。

問題2　盗人算
橋の下で盗人が盗んだ絹の反物を分け合っている声がする。「7反ずつとれば8反余り」「8反ずつとれば7反足らず」　さて、盗人は何人いるか。反物は何反あるか。

問題3　馬乗り算　
6里の道のりを4人で旅するとき、馬3頭に平等に交代で乗るとしたら一人あたり何里ずつ乗ればよいか。

江戸時代の算数


和算ノススメ
１．和算とは・・・江戸時代の数学
　日本の数学は、奈良時代の少し前から室町時代まではすべて中国から伝わったものでしたが、江戸時代、鎖国をしていた日本では、西洋の影響をほとんど受けない日本独自の数学が発達し、ヨーロッパ数学に匹敵するまでになりました。幕末から明治にかけて欧米から伝わった数学を「洋算」と呼ぶのに対して、その日本の数学を「和算」と呼びます。
　和算は、算盤などの、実用的な計算だけでなく、田を作り、水を引く土木工事や、天体観測して暦を決める暦法、商業などに大いに役立ちました。また、和算は一種の趣味、教養、道楽として好まれ、殿様、武士から商人、職人など庶民まで、あらゆる階層の人々が学んでいました。このことは世界でも稀な伝統文化の特徴として世界に誇れるものと言えます。

※『万葉集・巻十一』
　「若草の新手枕を巻き初めて夜をや隔たてむ二八十一（にくく・憎く）あらなくに」
　　十六・・・しし　　三五月・・・望月（十五夜）

※「和算」という呼び名が生まれるまでは、日本の数学は、ただ「算」とか,「算学」,「算術」,「算法」,「数学」などと呼ばれていました。

２．和算の教科書・・・江戸時代の超ベストセラー『塵劫記』
　現存する日本最古の数学書は、1600年頃に刊行された『算用記』(著者不明・龍谷大学蔵）ですが、続いて1662年に『割算書』が、1627年（元和8年）に『塵劫記』が出版されました。これらの書物の刊行は、算盤が一般庶民にかなり広まり、より高度な計算が必要とされてきた証と思われます。
　中でも、吉田光由（1598～1672）が著した『塵劫記』は、10版以上も改版されるほどの超ベストセラーとなり、庶民から武士まで、広く和算の教科書として親しまれました。『塵劫記』は、挿し絵入りの数学解説書、実用書で、4巻から成り、次のような内容が大変わかりやすく書かれています。
・大きい数及び小さい数の名・・・・万、億、兆、京・・・など
・度量衝や貨幣　・整数の性質　・比例　・利息算　・級数　・平方根及び立方根　・幾何図形　・相似形　・面積　・体積　・測量
これらのことは、日常に必要な問題の形にして書かれています。たとえば、
・米の売買のこと　・銭や小判の両替のこと　・船の運賃のこと　・升の寸法や容積のこと
そして、さらに人々が興味を持ちやすいように
・日に日に倍々のこと（阿波の長者の米粒問題）・継子立て（小石を30個並べて取っていく問題）・ねずみ算　・油分け算 ・百語減算

※『塵劫記』は、岩波文庫から出版されています。（青版24-1）
また『塵劫記』の研究書、解説書、授業に使える本なども数多く出版されています。
　
　『塵劫記』の続いて、または対抗して江戸時代には続々と数学書が出版されました。そして、それらには「遺願」または「好み」という"解答をつけない問題"が載せられ、読者にその解答を求める、という試みがなされるようになりました。（このように、言わばリレー式に問題、解答を繰り出すことを「遺願継承」と呼びます。）
　これは、当事さかんになった「算学塾」で数学を教えている者に相応の力があるかどうか、出題した問題を解くことで判定してほしいという作者からの挑戦状のようなものでしたが、このことは和算の発展、伝般に大きな役割を果たしました。

３．算額というもの
このような、和算の発展、流行を今に伝える物として「算額」があります。
「算額」とは、神社や仏閣に奉納したすうがくの絵馬のことです。江戸時代の中期、寛文年間の頃から始まった風習と言われ、現在、全国に約820面残っています。
算額は、数学の問題が解けたことを神仏に感謝し、ますます勉学に励むことを祈願して奉納されたものと思われます。問題を書いて解答をつけないで掲げるもの、その問題を見て解答を奉納するもの、当時さかんだった「算塾」が自分達の流派を宣伝するためのものなど内容はさまざまですが、人々は神仏の加護により解答が得られると考えていたようです。そこで、人も集まる神社仏閣が数学の発表の場となっていました。
　岡山県にも、14の神社、お堂にに算額が現存してしていますが、一番近いところでは美作国一宮である中山神社にあります。
　算額奉納の習慣は世界に例を見ない日本独自の文化です。明治になり、国家の近代化の必要性から洋算の導入が急がれましたが、それを容易にしたのもこの風習があったからこそと思われます。
先人が残してくれた貴重な文化遺産として、また、学問に対する真摯な姿勢を教えてくれる励ましとして、これらの算額を大切にし、子どもたちにも教え、後世に伝えたいものです。

４．世界的な大数学者、関　孝和
　幼い頃から「塵劫記」に親しみ、遺願継承で勉学に励み、後に日本を代表する数学者となったのが関　孝和（1640？～1708）です。
関　孝和の業績を上げればきりがありませんが、たとえば微分積分の発見、点鼠術という文字係数の代数式を筆算で表せるようにした代数記法、方程式の判別式、ニュートンの近似解法、行列式やベルヌイ数の発見、未知数の変換、正負の根の存在条件、極値論、近似分数、不定方程式の解法、正多角形や円周率に関する計算、ハップスギュルタンの法則、ニュートンの補間公式、方陣、円錐曲線論など難解な高等数学の発見や計算を行っています。
　中でも、彼が得意としていたのは立体幾何ですが、その基となった土壌体積の計算です。農業では、水田は絶対水平面が必要なのですが、傾斜の多い日本の土地では斜面を削って水平線を作らねばなりませんでした。その際に立体幾何が使われ、土壌の体積計算がなされました。関　孝和は武士であってもその高等数学は農民の日常生活に根ざすものが多く、彼の弟子も農民出身者が多いそうです。玉川用水、静岡の用水トンネル、箱根用水を作ったのは算額塾で学んだ農民です。（水がどこでも同じ速さで流れるようにするには高い知識と技術を必要とします。）水呑百姓だった二宮尊徳も、立体幾何をフルに使って地形を改良し、農業改革を行っています。

半円に直角三角形が内接している、この直角三角形の内接円と弓形内に描いた最大円が相等しいとき、外接円と小円の半径の関係を求めよ。
和算書「算法少女」より

５．和算の衰退...学校から和算が消えた日
　明治維新後、近代国家への変革を迫られた政府は、全国民を対象とする学校制度を整え、明治5年8月に「学制」を公布しました。その策定の過程で、公布直前まで政府の役人達が迷ったのが学校で教えるのに西洋数学と和算のどちらを採用するかでした。結局、日本を一日も早く近代化するには、西洋の数学を基礎から教育していく必要があるという結論に落ち着きました。
こうして伝統ある日本の数学は、国の再出発の時に学校教育から姿を消し、「過去の学問」となったのです。

６．再び光が...和算ブーム起こる
　明治以降、西洋数学中心の教育システムに切り替えられましたが、その一方では和算を守ろうという声が高まってきて研究が進んでいます。最近では、テレビのクイズ問題、大学の入試問題に採用されるなどちょっとした"和算ブーム"さえ起こっています。
小学校では、6年・下の教科書に次のような記述があります。

★研究機関、研究所
・和算研究所・和算の館・神奈川和算研究所（その他多数）
「和算で遊ぼう！＝江戸時代の庶民の娯楽＝」（佐藤健一著・かんき出版）
「江戸のミリオンセラー「塵劫記」の魅力＝吉田光由の発想＝」（佐藤健一著・研成社）
「文化史上より見たる日本の数学」（三上義夫著・岩波文庫）その他多数

7.子供達に和算を教え意義
（1）「おもしろい算数」との出会い
鶴亀算、盗人算、馬乗り算、ねずみ算、方陣、油分け算など
（2）ウンウン唸って考えることの楽しさを体験させる
"わかりやすい"ことも大切だが、長い時間をかけて、苦労しながら考えることもおもしろいものだ。
（3）算数を見る視点を変える
数学（和算）を、日本の伝統文化として見直し、数学に親しみ、考えることに真摯に取り組んだ先人の姿に学ぶ。
また、実用の数学が高等数学へと発展し、さらに高度なものになって実用性を高め、生活に役立つ知識や技術になったことを知る。
（資料提供：和田陽子さん）